已知N個相異物，取出m個的方法一共有
今寫一程式，當 N=4，m=2 時，將各種組合方法顯示出來。
輸出：
12
13
14
23
24
34

本文提供三種演算法供大家參考。

(1)二進位法
二進位法是利用二進位數值，0表示隱藏，1表示出現，將每一相異物，以二進位1個 bit 代替。因此 N 個相異物，就必須 N 個 bits 變數。
c 語言一個 int 變數佔用 4 bytes 空間，因此有 32 bits 可用，也就是可取代的相異物最大數量為 32。
程式為了限制記憶體使用量，因此問題侷限在 16 個相異物以下，也就是一個 int 變數就可以處理了。
以下為了說明方便，我們以 4 個 bits，代替 4 個相異物，如下說明：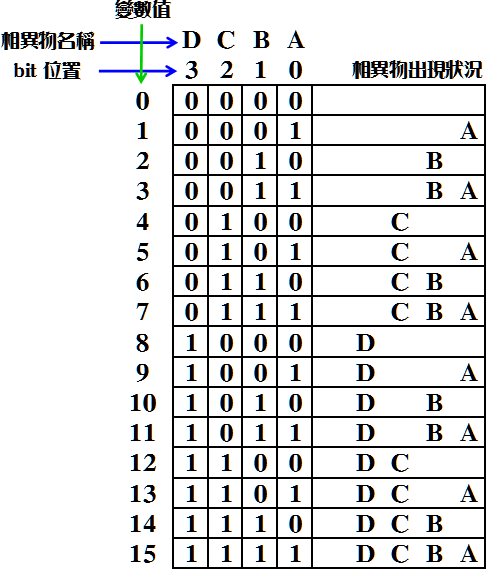

由上圖表可知 變數值由 1 至 15，就可以呈現 ABCD 四個相異物所有組合情形。
如果要篩選所有只出現2個相異物的情況，就必須從 1 至 15，每一個數字檢查所有 1 的數量，
將出現 2 個 1 的數字呈現出來即可。
由上表過濾，可得到下表：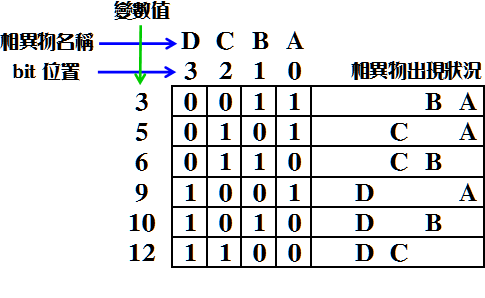

程式下載

(2)堆疊法
堆疊法是利用迴圈方式，計數器數值表示物件代號，因此 N 個
相異物，就必須 N 層迴圈，又因迴圈無法以動態方式依需求改
變層數，所以必須以堆疊模擬迴圈，以下是說明：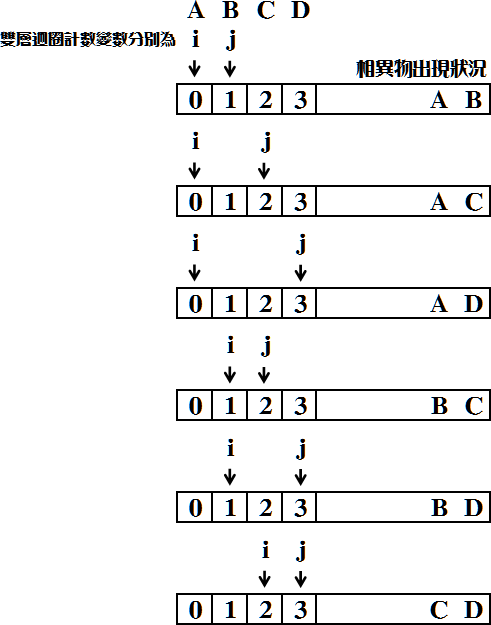


當 m=2 時，程式範例：
for(int i=0;i<n-1;i++)
    for(int j=i+1;j<n;j++)
        cout << char(i+int('A')) << char(j+int('A')) << endl;

當 m=3 時，程式範例：
for(int i=0;i<n-2;i++)
    for(int j=i+1;j<n-1;j++)
        for(int k=j+1;k<n;k++)
            cout << char(i+int('A')) << char(j+int('A')) << char(k+int('A')) << endl;

上面的例子，不同的 m 值，就有不同的 for 迴圈層數，若使用 if else
或 switch，篩選不一樣的 m 值對應不同的 for 層數，雖然可行，但程
式碼不少。今使用堆疊替代 for 迴圈，說明如下：



說明為何有些堆疊資料可以預測無法 push 程式碼如下：
例如：
假設 m=10，n=9，當 sp=4 時，要 push 的資料 j，為何? 就無法 push 了。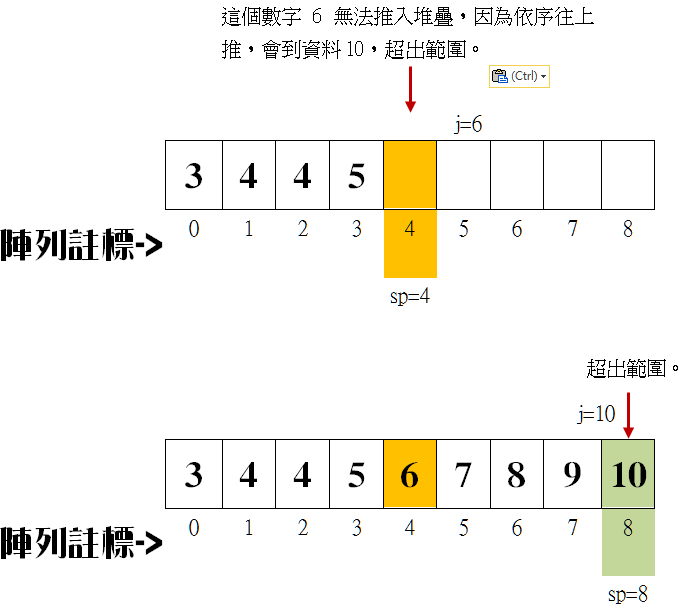

當 m=10 時，表示資料只能從 0 至 9，sp (stack point) 為堆疊指標，
也就是陣列註標指標，當 sp=4 時，可預測剩下的堆疊空間為 n-sp = 5
此時要 push 的資料總長度就不能超出 5 個，否則就超出範圍了。
然而如何計算要 push 的總資料長度? 要 push 的資料最大值為 m-1 = 9，
目前的資料是 j = 6，所以 9-6 + 1 (包含 6) = 4，

程式下載

(3)遞迴法
當 M5，N=3 時考慮下列情形：
N=1時：
{}
{1}
================
N=2，遞迴與上面合成：
{2}
{1,2}
================
N=3，遞迴與上面合成：
{3}
{1,3}
{2,3}
{1,2,3}
================
N=4，遞迴與上面合成：
{4}
{1,4}
{2,4}
{1,2,4}
{3,4}
{1,3,4}
{2,3,4}
{1,2,3,4}(此集合超出3，應去除)
================
N=5，遞迴與上面合成：
{5}
{1,5}
{2,5}
{1,2}
{3,5}
{1,3,5}
{2,3,5}
{1,2,3,5}(此集合超出3，應去除)
{4,5}
{1,4,5}
{2,4,5}
{1,2,4,5}(此集合超出3，應去除)
{3,4,5}
{1,3,4,5}(此集合超出3，應去除)
{2,3,4,5}(此集合超出3，應去除)

整理後得到結果為：
{}
{1}
{2}
{1,2}
{3}
{1,3}
{2,3}
{1,2,3}
{4}
{1,4}
{2,4}
{1,2,4}
{3,4}
{1,3,4}
{2,3,4}
{5}
{1,5}
{2,5}
{1,2,5}
{3,5}
{1,3,5}
{2,3,5}
{4,5}
{1,4,5}
{2,4,5}
{3,4,5}

過濾掉不是 3 元素，剩下
{1,2,3}
{1,2,4}
{1,3,4}
{2,3,4}
{1,2,5}
{1,3,5}
{2,3,5}
{1,4,5}
{2,4,5}
{3,4,5}

程式下載