是一種組合優化的 NP 完全問題。問題可以描述為:給定一組物品,
每種物品都有自己的價格及重量,在限定的總重量內,我們如何選擇,
才能使得物品的總價格最高。
問題的名稱來源於如何選擇最合適的物品放置於給定背包中。相似
問題經常出現在商業、組合數學,計算複雜性理論、密碼學和應用數學
等領域中。也可以將背包問題描述為決定性問題,即在總重量不超過 W
的前提下,總價值是否能達到 V。
以下是各問題的探討:
可分割物品之解決方案:
假設某小偷帶了一個 2000 cc 的容器,準備要到某家酒店偷酒,
下列是這家酒店內,可偷的酒價格與容量,每樣酒可以使用小塑膠
袋盛裝,再放入容器,假設塑膠袋不暫空間,請問小偷要如何偷到
總價值最高的酒? (容器可以不裝滿)(酒可以開瓶分裝)
| 酒名 | 價格 ($) | 每瓶容量(cc) | 剩餘數量(瓶) |
|---|---|---|---|
| 白蘭地Brandy | 1380 | 300 | 2 |
| 葡萄酒 Wine | 2800 |
700 |
2 |
| 威士忌 Whisky | 1400 |
320 |
1 |
| 香檳Champagne | 1800 |
500 |
5 |
| 台灣陳年高粱 | 600 |
600 |
20 |
此題因可分裝,所以可以開瓶分割內容物,因此先計算每種酒
每 cc 最高價值,再由最高者取捨。(見下表)
| 酒名 | 價格 ($) | 每瓶容量(cc) | 每cc價格 | 剩餘數量(瓶) | 總 cc 數 |
|---|---|---|---|---|---|
| 白蘭地Brandy | 1380 | 300 |
4.6 | 2 |
600 |
| 葡萄酒 Wine | 2800 |
700 |
4 | 2 |
2800 |
| 威士忌 Whisky | 1400 |
320 |
4.375 | 1 |
320 |
| 香檳Champagne | 1800 |
500 |
3.6 | 5 |
2500 |
| 台灣陳年高粱 | 600 |
600 |
1 | 20 |
12000 |
最後結論:
白蘭地 (600cc) + 威士忌 (320cc) + 葡萄酒 (1080cc) = 2000cc
價值:
白蘭地 (4.6$ × 600cc) + 威士忌 (4.375$ × 320cc) +
葡萄酒 (4$ × 1080cc) = 8480$ (平均每 cc 4.2$
由上可知,可分割物品,貪婪法就可解決,沒什麼高深學問可以討論。
不可分割物品之解決方案:
請思考下列問題:
假設某小偷帶了一個背包,準備要到某位富有人家偷東西,下列是
這富人房內物品資訊。因小偷體力有限,因此不可能無限制將所有物
品搬走,假設小偷只能負重 20 公斤的物品,且每樣物品不可分割,則
小偷要偷哪些東西,總價值最高?
| 物品名稱 | 價值 | 物品重量 | 物品數量 |
|---|---|---|---|
| 不鏽鋼圓缸 | 76 | 17 | 2 |
| 金壺 | 55 |
12 |
2 |
| 銀盆 | 45 |
10 |
2 |
| 青銅小鼎 | 34 |
8 |
2 |
| 陶瓷馬克杯 | 13 |
3 |
2 |
今計算每件物品的 價值/每公斤 ,如下表:
| 物品名稱 | 價值 | 物品重量 | 物品數量 | 價值/每公斤 |
|---|---|---|---|---|
| 不鏽鋼圓缸 | 76 | 17 |
2 |
4.471 |
| 金壺 | 55 |
12 |
2 |
4.583 |
| 銀盆 | 45 |
10 |
2 |
4.5 |
| 青銅小鼎 | 34 |
8 |
2 |
4.25 |
| 陶瓷馬克杯 | 13 |
3 |
2 |
4.333 |
依照貪婪法,由最高價值金壺先拿,但 1 個金壺重 12,無法同時拿
2 個因此剩下 8 公斤就拿青銅小鼎,總價值 55 + 34 = 89
另一種取法,隨便亂取,只要把重量撐到 20 就好,
銀盆 2 個恰好 20 公斤,價值 45 × 2 = 90 ,
天啊~~ 隨便亂取居然比貪婪法優,因此怎麼取物品是有學問的。
以下使用暴力法解看看,
下列程式使用變數內容說明
| 物品名稱 | 拿取數量 |
|---|---|
| 不鏽鋼圓缸 | a0 |
| 金壺 | a1 |
| 銀盆 | a2 |
| 青銅小鼎 | a3 |
| 陶瓷馬克杯 | a4 |
拿取物品後,總重量 wT
拿取物品後,總價值 s
到目前為止,最大價值 max
最大價值 max 的組合敘述,Label1.Text
設定最大負重為 Const MaxLoad = 20
w() 陣列放置所有物品重量
v() 陣列放置所有物品價值
物品所剩數量均設為 2
重要指令說明
MaxLoad \ w(0) : 表示第一件物品,在 MaxLoad 的限制下,最大能拿取數。(以下依此類推)
Math.Min(MaxLoad \ w(0), 2) : 表示第一件物品,能拿取數與物品剩餘數,選最小的。
意思就是說,最大能拿取 3 件,可是物品才 2 件,最後也只能拿 2 件。
If (wT<= MaxLoad) Then : 表示所拿物品總重量,必須判斷是否超重。
If (max < s) Then : 表示所拿物品總重量,是否比上次拿的更重,是的話就記錄。
For a0 = 0 To Math.Min(MaxLoad \ w(0), 2)
For a1 = 0 To Math.Min(MaxLoad \ w(1), 2)
For a2 = 0 To Math.Min(MaxLoad \ w(2), 2)
For a3 = 0 To Math.Min(MaxLoad \ w(3), 2)
For a4 = 0 To Math.Min(MaxLoad \ w(4), 2)
wT= w(0) * a0 + w(1) * a1 + w(2) * a2 + w(3) * a3 + w(4) * a4
If (wT<= MaxLoad) Then
s = v(0) * a0 + v(1) * a1 + v(2) * a2 + v(3) * a3 + v(4) * a4
If (max < s) Then '比上次拿的重就記錄
max = s
Label1.Text = If(a0 > 0, a0 & ":" & v(a0) & "*" & a0, "") &
If(a1 > 0, a1 & ":" & v(a1) & "*" & a1, "") &
If(a2 > 0, a2 & ":" & v(a2) & "*" & a2, "") &
If(a3 > 0, a3 & ":" & v(a3) & "*" & a3, "") &
If(a4 > 0, a4 & ":" & v(a4) & "*" & a4, "") & " = " & s
End If
End If
Next
Next
Next
Next
Next
這個演算法,若物品少,還可試一試,萬一物品有 10 個,那麼光是 for 迴圈就 10 層,
如果每樣東西可拿到 10 件,那麼每層迴圈就 For an = 0 To 10 ,共 11 次,所以共
有 1110搜尋次數,所以當物品很多時,就要考慮動態規劃法(Dynamic Programming),
雖然動態規劃法,也不能解大數據 NP 問題,但至少比上例暴力法優。
在介紹動態規劃法前,先介紹活的迴圈控制敘述。依照上例,5 個物品需要 5 層迴圈,
寫起來有點笨重,萬一十層迴圈,那該如何?
下面例子假設 5 層迴圈狀況如表:
計數器變數名 |
起始植 |
終止值 |
a0 |
2 |
5 |
a1 |
5 |
5 |
a2 |
3 |
4 |
a3 |
0 |
2 |
a4 |
4 |
5 |
程式如下:
For a0 = 2 To 5
For a1 = 5 To 5
For a2 = 3 To 4
For a3 = 0 To 2
For a4 = 4 To 5
ListBox1.Items.Add(a0 & ":" & a1 & ":" & a2 & ":" & a3 & ":" & a4)
Next
Next
Next
Next
Next
今考慮堆疊使用
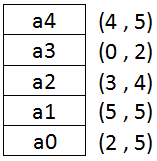
1.上層 a4 必須從 4 至 5 (每次都以 pop 方式 +1 後再 push 入堆疊)。
2.當 a4 到達 5 以後,才能 pop 底層 a3。
3.a3 pop 出來後,跟 a4 運作一樣,pop +1 後再 push 入堆疊。
4.當 a3 被 pop +1 以後,再 push 入堆疊,此時 a4 必須從頭開始,並 push 入堆疊。
5.a4 以下變數模式相同,直到 a0 = 5 為止。
6.此方式,使用到 10 層迴圈程式碼也不會很長。
Dim ForTable(4, 1) As Integer, i As Integer, s As String = "", j As Integer
ForTable(0, 0) = 2 : ForTable(0, 1) = 5
ForTable(1, 0) = 5 : ForTable(1, 1) = 5
ForTable(2, 0) = 3 : ForTable(2, 1) = 4
ForTable(3, 0) = 0 : ForTable(3, 1) = 2
ForTable(4, 0) = 4 : ForTable(4, 1) = 5
For i = 0 To 4 '先將所有變數起始值推入堆疊
push(ForTable(i, 0))
Next
i = 0
Do While (True)
s = ""
For j = 0 To 4
s &= j & ":" & stack(j) & " "
Next
ListBox1.Items.Add(s) '這是 for 回圈內要做的事,在此只是列印 a0 ~ a4 輸出變數內容至 ListBox1 而已
Do '每次變數倒底,就必須再 pop 出來,直到堆疊沒了且最後變數也到底了
i = pop() + 1 '取出堆疊後+1
Loop While ((i > ForTable(sp, 1)) And Not ((sp = 0) And i > ForTable(sp, 1)))
If ((sp = 0) And i > ForTable(sp, 1)) Then '堆疊到底表是變數已到 a0
Exit Do '完工
Else
push(i) '取出堆疊後+1, 再推入堆疊
For j = sp To 4
push(ForTable(sp, 0)) '若是取到 a4 以前, 則以後的變數重新開始
Next
End If
Loop
最後要說明動態規劃的方式了。
遞迴版動態規劃背包問題
假設物品編號為 0 ~ n
假設背包遞迴程式為 Knapsack( p , x)
表示可負重 x 點數,並把 p ~ n 的物品,選出最高價值,放入包包內
要使效率提高,最好準備一陣列,記錄 Knapsack( p , x) 的值,也就是用空間換取搜尋時間。