演算法(Algorithm)的定義
從輸入到輸出的解題步驟
演算法是一組明確的指令步驟,用於解決某個問題或完成特定任務。
可以把它想成:從「輸入」到「輸出」的一條路線圖,必須在有限時間內完成,且結果要正確、可預測。
演算法是一組明確的指令步驟,用於解決某個問題或完成特定任務。
可以把它想成:從「輸入」到「輸出」的一條路線圖,必須在有限時間內完成,且結果要正確、可預測。
很多「看起來不同」的應用,其實背後用的是同一種演算法。
例:排序學會一次,就能用在成績、價格、時間等各種資料。
問題:給定一個整數 n,若是質數則輸出 Yes,否則輸出 No。
先不要急著寫程式,先用步驟想一想:
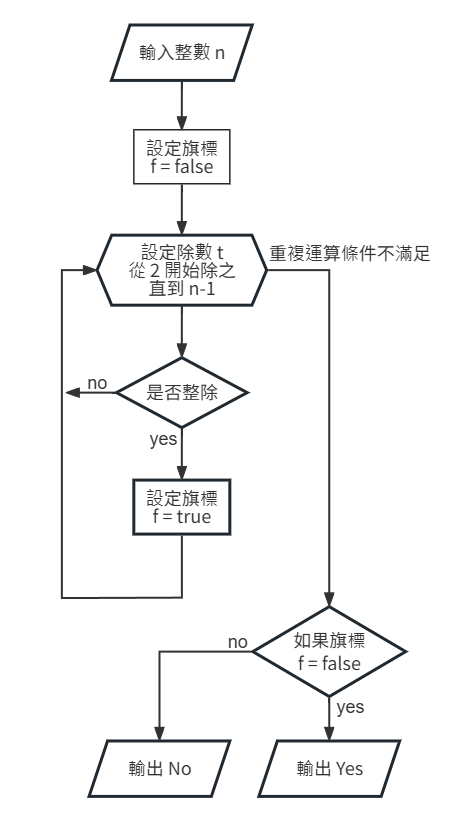
步驟(第一版):
f = false。f = true。f = false,則輸出 Yes,否則輸出 No。流程圖(第一版):
顯示/隱藏:優化思路
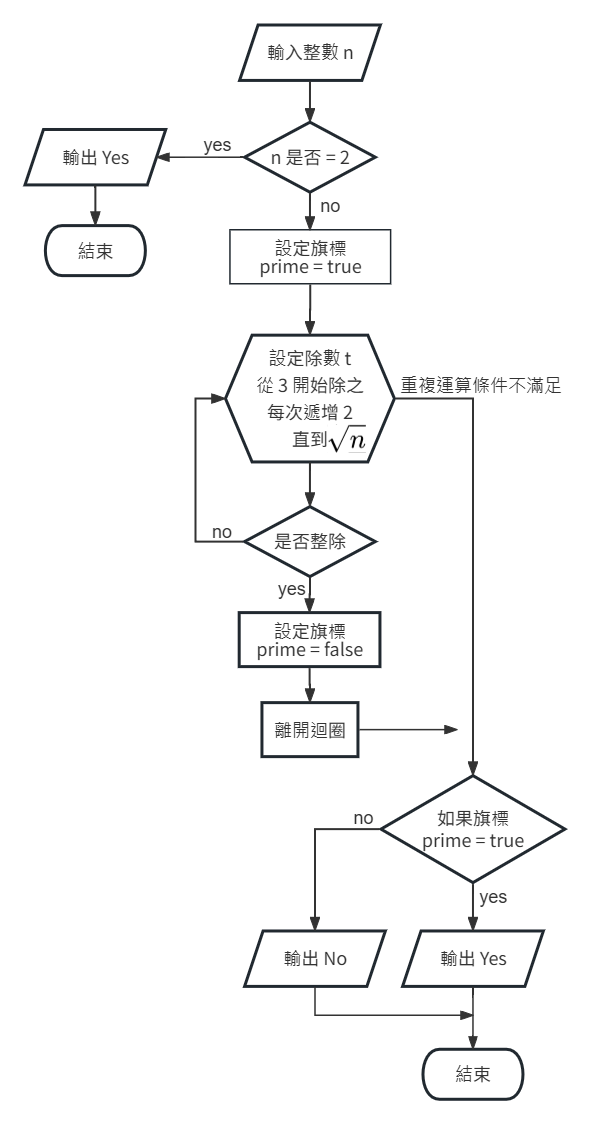
prime。步驟(優化版):
prime = true。prime = false,並離開迴圈。重複步驟 4,直到除數 = $$\text{int}(\sqrt{n})$$。
prime = true 則輸出 Yes,否則輸出 No。流程圖(優化版):