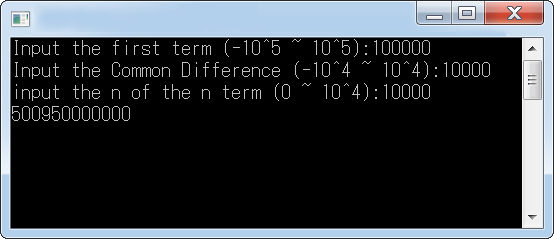
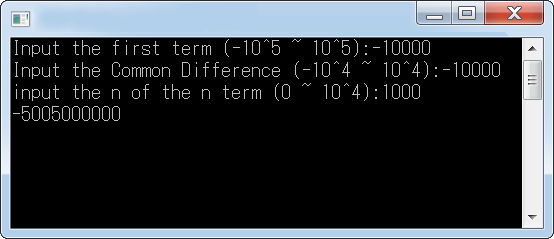
1. 請使用迴圈，寫一求等差數列程式，輸入首項 a(範圍-105 至 105整數)，公差 d(範圍-104 至 104整數)，項數 n(範圍 0 至 104整數)，輸出 s
(註：首項 (first term)、公差(Common Difference)、n 項(n term) )





【參考答案】
2. 已知費波那契數列(義大利語：Successione di Fibonacci) 定義：
1.F(1)=1
2.F(2)=2
3.F(n)=F(n-1)+F(n-2) (n≥3)
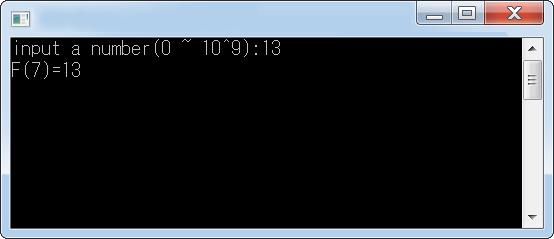
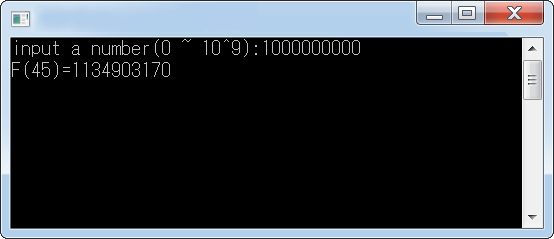
請寫一程式，輸入一正整數 K(範圍 0 至 109整數)，求出費氏數列第 N 項之值及N (需大於K且接近K)



【參考答案】
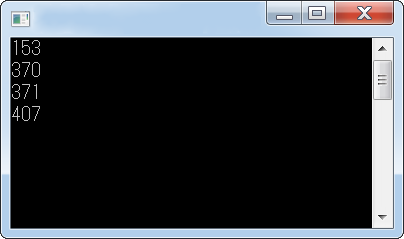
3. 寫一求等比數列程式，輸入首項 a(範圍-102 至 102浮點數)，公比 r(範圍-3 至 3浮點數)，項數 n(範圍  0 至 30 浮點數)
4. 假若一 3 位數的正整數，若此正整數的每一位數的 3 次方和，恰等於該正整數，則該正整數稱為三位數的 Armstrong (阿姆斯壯數)。
例如：153=13+53+33
寫一程式，找出所有 3 位數的阿姆斯壯(Armstrong)數。

【參考答案】
5. 假若一 n 位數的正整數，若此正整數的每一位數的 n 次方和，恰等於該正整數，則該正整數稱為 Armstrong (阿姆斯壯數)。
例如：，則 153 為阿姆斯壯數。
請寫一程式輸入 n (2≤n≤5)，程式找出 n 位數所有的 Armstrong，並統計阿姆斯壯數的個數。
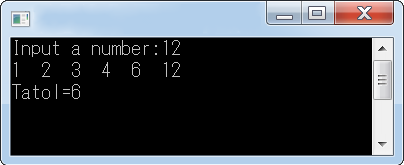
6. 寫一程式，輸入一正整數 N(範圍 0 至 109整數)找出該數所有的因數。
例如：
12 的因數為 1,2,3,4,6,12



【參考答案】
7. 呈上題，若所有因數和恰等於 N ，則該數成稱為完美數，
請輸入K(範圍 0 至 109整數)，並找出 2 至 K 所有的完美數.
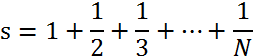8. 寫一程式計算 ，當s>2時停止，並顯示 s 與 N
9. 假若一正整數，若此正整數洽為該正整數因數(不包含自己本身)之和，則此正整數稱為完美數，例如正整數 6 的因數為 1、2、3、6，去掉6(自身)，則 6=1+2+3，所以 6 為完美數。
請寫一程式輸入 n (2≤n≤10000)，程式找出 1 至 n 所有的完美數，並統計完美數的個數。
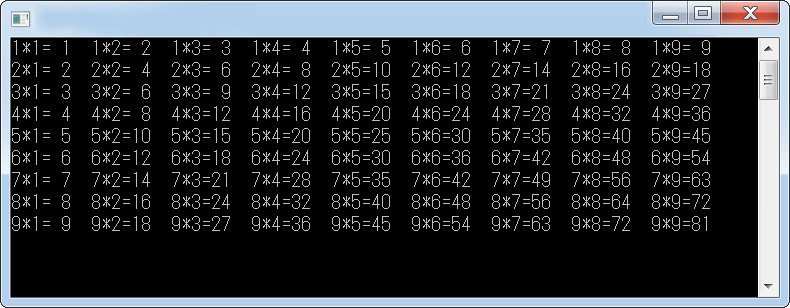
10. 寫出如下圖的 9×9 乘法表(並用 for、while、do while 三種迴圈完成)



【參考答案】
11. 寫出如下圖的 9×9 乘法表(並用 for、while、do while 三種迴圈完成)
12. 寫一程式，輸入 n，程式依據 n 值輸出圖形。如下例：
n=5 時，
    1
   21
  321
 4321
54321



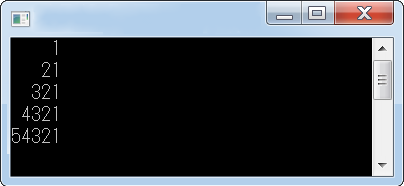
【參考答案】
13. 寫一程式，輸入 n，程式依據 n 值輸出圖形。如下例：
n=5 時，
        1        
      2 1 2      
    3 2 1 2 3    
  4 3 2 1 2 3 4  
5 4 3 2 1 2 3 4 5
  4 3 2 1 2 3 4  
    3 2 1 2 3    
      2 1 2      
        1        
14. 寫一程式，輸入 n，程式依據 n 值輸出圖形。如下例：
n=5 時，
1 2 3 4 5 4 3 2 1
  1 2 3 4 3 2 1  
    1 2 3 2 1    
      1 2 1      
        1        
      1 2 1      
    1 2 3 2 1    
  1 2 3 4 3 2 1  
1 2 3 4 5 4 3 2 1


15. 寫一程式，輸入 n，程式依據 n 值輸出圖形。如下例：
n=5 時，
A A A A A A A A A
A B B B B B B B A
A B C C C C C B A
A B C D D D C B A
A B C D E D C B A
A B C D D D C B A
A B C C C C C B A
A B B B B B B B A
A A A A A A A A A