函數原型
int sign(int)
說明:
傳入:整數
傳回:整數
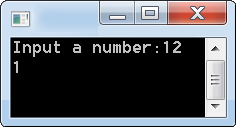
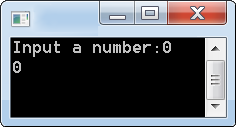
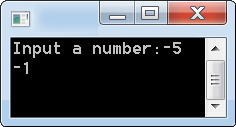
功能:判斷傳入的整數,若 N > 0 傳回 1,N = 0 傳回 0,N < 0 傳回 -1。
使用範例:
int a;
scanf("%d",a);
printf("%d\n", sign(a));
將下列程式碼 (Dev C++ 版本),複製至你的程式碼,並在副程式部份填入你的程式碼。
#include <stdio.h>
#include <stdlib.h>
int sign(int a){
//寫下你的程式碼
}
int main(int argc, char *argv[]) {
int a;
printf("Input a number:");
scanf("%d",&a);
printf("%d\n",sign(a));
return 0;
}
函數原型
float average2(int , int)
說明:
傳入:三整數
傳回:三整數的平均值。
使用範例:
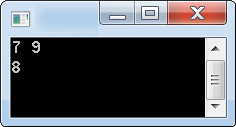
cin >> x >> y;
cout << average2(x,y);
將下列程式碼 (Dev C++ 版本),複製至你的程式碼,並在副程式部份填入你的程式碼。
#include <iostream>
using namespace std;
float average2(int a , int b){
//寫下你的程式碼
}
int main(int argc, char** argv) {
int x,y;
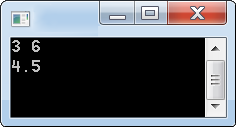
cin >> x >> y;
cout << average2(x , y);
return 0;
}
解答
函數原型
float average3(int , int , int)
說明:
傳入:三整數
傳回:三整數的平均值,並四捨五入至小數第一位。
使用範例:
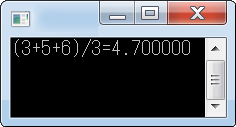
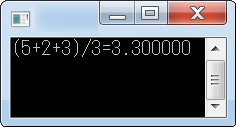
float x=average3(3, 5 ,6);
printf("(3+5+6)/3=%f\n", x);
#include <iostream>
using namespace std;
float average2(int a , int b){
//寫下你的程式碼
}
int main(int argc, char** argv) {
int x,y;
cin >> x >> y;
cout << average2(x , y);
return 0;
}
解答
函數原型
int Sum(int)
說明:
計算 1 至 N 的等差數列和。
傳入
一整數 N
傳回
傳回 1 至 N 的等差數列和。
使用範例:
cout << Sum(10); //計算 1+2+3+...+10 = 55
將下列程式碼 (Dev C++ 版本),複製至你的程式碼,並在副程式部份填入你的程式碼。
#include <stdio.h>
#include <stdlib.h>
int Sum(int n){
//寫下你的程式碼
}
int main(int argc, char *argv[]) {
int n;
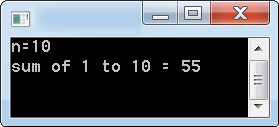
printf("n=%d");scanf("%d",&n);
printf("sum of 1 to %d = %d\n",n , Sum(n));
}
解答
函數原型
long long Factorial(int)
說明:
計算 1 至 N 的等差數列和。
傳入
一整數 N
傳回
傳回 1 至 N 的等差數列和。
使用範例:
cout << Factorial(10); //計算 1+2+3+...+10 = 3628800
將下列程式碼 (Dev C++ 版本),複製至你的程式碼,並在副程式部份填入你的程式碼。
#include <stdio.h>
#include <stdlib.h>
int Factorial(int n){
//寫下你的程式碼
}
int main(int argc, char *argv[]) {
int n;
printf("n=");
scanf("%d",&n);
printf("Factorial of 1 to %d = %lld\n",n , Factorial(n));
}
解答
函數原型
int Gcd(int a, int b)
說明:
傳入兩正整數 a 與 b,函數傳回 a 與 b 的最大公因數。(a b 均不為零,且不超出 int 範圍 2,147,483,647)
傳入
兩正整數
傳回
兩正整數之最大公因數
使用範例:
int a,b;
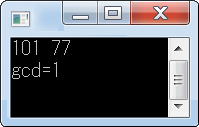
scanf("%d %d",&a, &b);
printf("gcd=%d\n", Gcd(a,b));
將下列程式碼 (Dev C++ 版本),複製至你的程式碼,並在副程式部份填入你的程式碼。
#include <stdio.h>
#include <stdlib.h>
int Gcd(int a , int b){
//寫下你的程式碼
}
int main(int argc, char *argv[]) {
int n;
printf("a=%d");scanf("%d",&a);
printf("b=%d");scanf("%d",&b);
printf("a and b gcd is %d\n",n , Gcd(a , b));
}
解答
| (註:已知 a , b 均不為零,則 a 與 b 之 Lcm = |
函數原型
long long Lcm(int a, int b)
說明:
傳入兩正整數 a 與 b,函數傳回 a 與 b 的最小公倍數。(a b 均不為零,且不大於 106)
傳入
兩正整數
傳回
兩正整數之最小公倍數
使用範例:
int a,b;
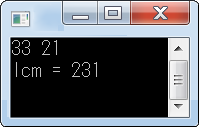
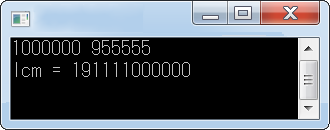
scanf("%d %d",&a, &b);
printf("lcm = %lld\n",lcm(a,b));
解答
函數原型
int isPrime(int n)
說明:
數學上質數的定義為:除了自己本身 與 1 之外,無其他自然數可以將整除自己者,該數稱為質數(Prime number)。
傳入
一整數。(整數不大於 int 範圍 2,147,483,647)
傳回
若該數為質數,則傳回 1,否則傳回 0。
使用範例:
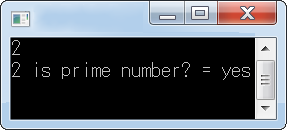
scanf("%d", &n);
printf("%d is prime number? = %s\n",n , ((isPrime(n))?"yes":"no"));
解答
函數原型
int prime(int n)
說明:
傳入一正整數 n (不大於 106)程式傳回自然數中第 n 位質數。
因此,prime(1) = 2
prime(2) = 3
prime(3) = 5
..................
prime(1000000) = 15485863
傳入
一正整數 n
傳回
自然數中第 n 位質數。
使用範例:
int n;
scanf("%d", &n);
printf("prime(%d) = %d\n", n, prime(n));
解答1 解答2