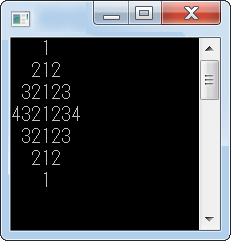
設定 n 為常數值 3
當輸入 3 時,印出 2*n-1 的方陣
1 |
||||
2 |
1 |
2 |
||
3 |
2 |
1 |
2 |
3 |
2 |
1 |
2 |
||
1 |
輸出範圍關係為 1 至 2*n-1
改變範圍 0-2*(n-1)
分析每個座標關係
(0,0) |
(1,0) |
(2,0) |
(3,0) |
(4,0) |
(0,1) |
(1,1) |
(2,1) |
(3,1) |
(4,1) |
(0,2) |
(1,2) |
(2,2) |
(3,2) |
(4,2) |
(0,3) |
(1,3) |
(2,3) |
(3,3) |
(4,3) |
(0,4) |
(1,4) |
(2,4) |
(3,4) |
(4,4) |
若看不出端倪,可以改變範圍標示。
從 0 至 2*n-1 改成 -(n-1) 至 (n-1)
並取絕對值。(只需該變 x 值即可)
(2,0) |
(1,0) |
(0,0) |
(1,0) |
(2,0) |
(2,1) |
(1,1) |
(0,1) |
(1,1) |
(2,1) |
(2,2) |
(1,2) |
(0,2) |
(1,2) |
(2,2) |
(2,3) |
(1,3) |
(0,3) |
(1,3) |
(2,3) |
(2,4) |
(1,4) |
(0,4) |
(1,4) |
(2,4) |
若再看不出端倪,可以再改變範圍標示。
設定 y 值為 -(n-1) 至 (n-1) 並取絕對值。
設定 x 值範圍與 y 值互補。
所謂互補即 x+y=n-1。
演算法:
i from -(n-1) to (n-1)
y=abs(i)
j from -(n-1) to (n-1)
x=n-abs(j)-1
|
|
由上可觀察出 當 x>=y 時
須顯示字元,此字元可分析如下:
x值 |
顯示值 |
2 |
1 |
1 |
2 |
0 |
3 |
發現顯示值與 x 互補,即 x + 顯示值 = 3 (n=3)
得 顯示值 = 3-x = n-x
因此程式碼如下:
int i,j,x,y,n=4;
for(i=-(n-1);i<=n-1;i++){
y=abs(i);
for(j=-(n-1);j<=n-1;j++){
x=n-abs(j)-1;
if(x>=y){
printf("%d",n-x);
}
else{
printf(" ");
}
}
printf("\n");
}