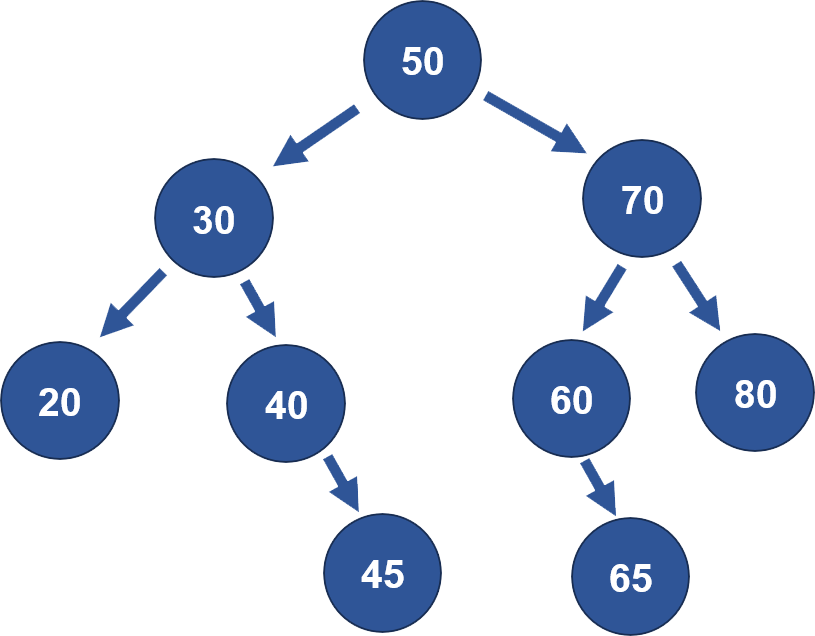
Binary Tree 是一種數據結構，其中每個節點最多有兩個子節點，分別稱為左子節點和右子節點。
每個節點包含一個數據元素，可以是任意型別，並且這些元素之間有特定的順序。
二元樹的結構使得查找、插入和刪除元素等操作更加高效。
根據二元樹的特性，左子樹的所有節點的值均小於根節點的值，而右子樹的所有節點的值均大於根節點的值。
以下是二元樹的一些常見術語：
  • Root：
    • 表示二元樹的根節點。每一個二元樹都有一個根節點，它是整棵樹的起點。
    Root
    public Node Root { get; private set; }

以下是雙向鏈接提供的方法：
  1. Insert(T data)：
    2. 將指定的數據插入二元樹中。這是一個公開方法，用於向樹中添加新的節點。
    Insert
    public void Insert(T data)
{
    Root = InsertRecursive(Root, data);
}

  2. InOrderTraversal()：
    3. 遞歸地執行中序遍歷，按左、根、右的順序輸出樹中的節點。
    InOrderTraversal
    public void InOrderTraversal()
{
    Console.Write("In-Order Traversal: ");
    InOrderTraversalRecursive(Root);
    Console.WriteLine();
}

  3. InsertRecursive(Node root, int data)：
    4. 遞歸地在樹中的指定位置插入節點。這是一個私有方法，用於實際執行插入操作。
    InsertRecursive
    private Node InsertRecursive(Node root, int data)
{
    if (root == null)
    {
        return new Node(data);
    }

    if (data < root.Data)
    {
        root.Left = InsertRecursive(root.Left, data);
    }
    else if (data > root.Data)
    {
        root.Right = InsertRecursive(root.Right, data);
    }

    return root;
}

  4. InOrderTraversalRecursive(Node root)：
    5. 遞歸地執行中序遍歷，按左、根、右的順序輸出樹中的節點。這是一個私有方法，用於實際執行中序遍歷。
    InOrderTraversalRecursive
    private void InOrderTraversalRecursive(Node root)
{
    if (root != null)
    {
        InOrderTraversalRecursive(root.Left);
        Console.Write(root.Data + " ");
        InOrderTraversalRecursive(root.Right);
    }
}

  5. BFS：
    6. 廣度優先搜尋（Breadth-First Search，簡稱 BFS）
    它以廣度為優先的方式進行搜尋，即先訪問同一層的所有節點，再進入下一層。
    Breadth-First Search
    binaryTree.BFS();

  6. DFS：
    7. 深度優先搜尋（Depth-First Search，簡稱 DFS）
    DFS 的基本思想是從起始節點出發，儘可能深入地訪問每一條分支，直到無法再深入為止，然後回溯到前一個節點，繼續深入其他分支。
    Depth-First Search
    binaryTree.DFS();

綜合範例
深度優先搜尋（Depth-First Search，簡稱 DFS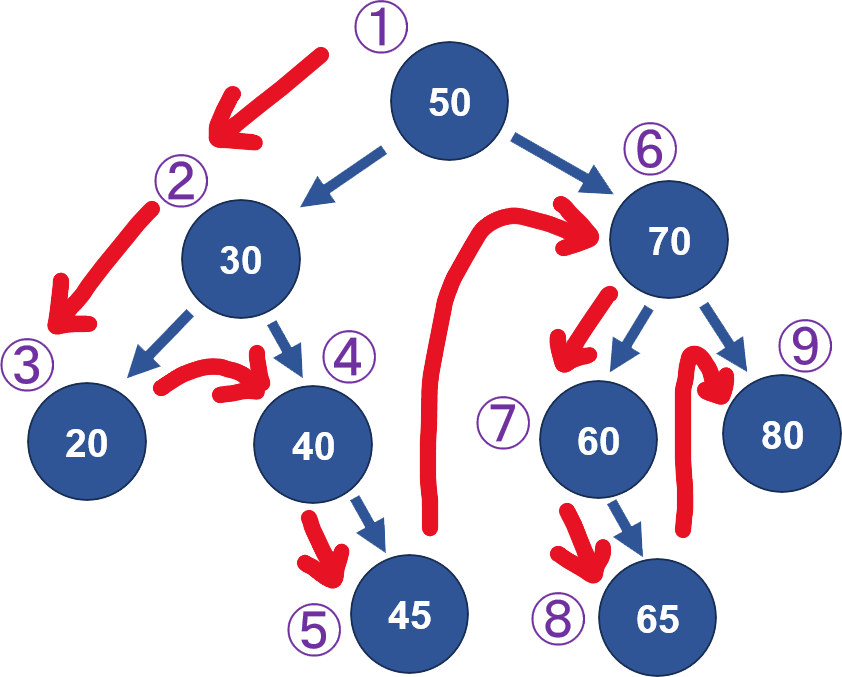
廣度優先搜尋（Breadth-First Search，簡稱 BFS）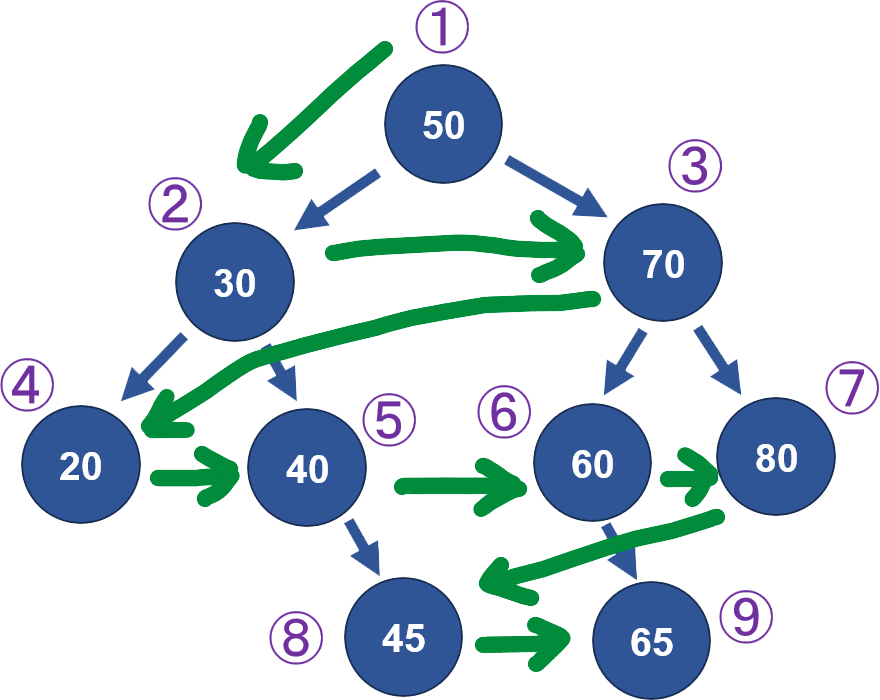


using System;
using System.Collections.Generic;
class Node
{
    public int Data { get; set; }
    public Node Left { get; set; }
    public Node Right { get; set; }

    public Node(int data)
    {
        Data = data;
        Left = null;
        Right = null;
    }
}
class BinaryTree
{
    public Node Root { get; private set; }

    public BinaryTree()
    {
        Root = null;
    }
    /// <summary>
    /// 將指定的數據插入二元樹中。這是一個公開方法，用於向樹中添加新的節點。
    /// </summary>
    /// <param name="data"></param>
    public void Insert(int data)
    {
        Root = InsertRecursive(Root, data);
    }
    /// <summary>
    /// 遞歸地在樹中的指定位置插入節點。這是一個私有方法，用於實際執行插入操作。
    /// </summary>
    /// <param name="root"></param>
    /// <param name="data"></param>
    /// <returns>傳回加入結點的二元樹</returns>
    private Node InsertRecursive(Node root, int data)
    {
        if (root == null)
        {
            return new Node(data);
        }

        if (data < root.Data)
        {
            root.Left = InsertRecursive(root.Left, data);
        }
        else if (data > root.Data)
        {
            root.Right = InsertRecursive(root.Right, data);
        }
        return root;
    }
    /// <summary>
    /// 遞歸地執行中序遍歷，按左、根、右的順序輸出樹中的節點。
    /// </summary>
    public void InOrderTraversal()
    {
        Console.Write("In-Order Traversal: ");
        InOrderTraversalRecursive(Root);
        Console.WriteLine();
    }
    /// <summary>
    /// 遞歸地執行中序遍歷，按右、根、左的順序輸出樹中的節點。
    /// </summary>
    public void ReverseOrderTraversal()
    {
        Console.Write("Reverse-Order Traversal: ");
        ReverseOrderTraversalRecursive(Root);
        Console.WriteLine();
    }
    /// <summary>
    /// 遞歸地執行中序遍歷，按右、根、左的順序輸出樹中的節點。(由大至小輸出)
    /// </summary>
    /// <param name="root"></param>
    private void ReverseOrderTraversalRecursive(Node root)
    {
        if (root != null)
        {
            ReverseOrderTraversalRecursive(root.Right);
            Console.Write(root.Data + " ");
            ReverseOrderTraversalRecursive(root.Left);
        }
    }
    /// <summary>
    /// 遞歸地執行中序遍歷，按左、根、右的順序輸出樹中的節點。(由小至大輸出)
    /// </summary>
    /// <param name="root"></param>
    private void InOrderTraversalRecursive(Node root)
    {
        if (root != null)
        {
            InOrderTraversalRecursive(root.Left);
            Console.Write(root.Data + " ");
            InOrderTraversalRecursive(root.Right);
        }
    }
    /// <summary>
    /// 廣度優先搜尋（Breadth-First Search，簡稱 BFS）
    /// </summary>
    public void BFS()
    {
        Console.Write("BFS Traversal: ");
        if (Root == null)
            return;
        Queue<Node> queue = new Queue<Node>();
        queue.Enqueue(Root);
        while (queue.Count > 0)
        {
            Node current = queue.Dequeue();
            Console.Write(current.Data + " ");

            if (current.Left != null)
                queue.Enqueue(current.Left);
            if (current.Right != null)
                queue.Enqueue(current.Right);
        }
        Console.WriteLine();
    }
    /// <summary>
    /// 深度優先搜尋（Depth-First Search，簡稱 DFS）
    /// </summary>
    public void DFS()
    {
        Console.Write("DFS Traversal: ");
        DFSRecursive(Root);
        Console.WriteLine();
    }
    /// <summary>
    /// DFS 遞迴搜尋
    /// </summary>
    /// <param name="root"></param>
    private void DFSRecursive(Node root)
    {
        if (root != null)
        {
            Console.Write(root.Data + " ");
            DFSRecursive(root.Left);
            DFSRecursive(root.Right);
        }
    }
}
class Program
{
    static void Main()
    {
        BinaryTree binaryTree = new BinaryTree();
        binaryTree.Insert(50);
        binaryTree.Insert(30);
        binaryTree.Insert(70);
        binaryTree.Insert(20);
        binaryTree.Insert(40);
        binaryTree.Insert(60);
        binaryTree.Insert(80);
        binaryTree.Insert(45);
        binaryTree.Insert(65);
        binaryTree.BFS();  // Output: 50 30 70 20 40 60 80 45 65
        binaryTree.DFS();  // Output: 50 30 20 40 45 70 60 65 80
        binaryTree.InOrderTraversal(); // Output: 20 30 40 45 50 60 65 70 80
        binaryTree.ReverseOrderTraversal(); // Output: 80 70 65 60 50 45 40 30 20
    }
}
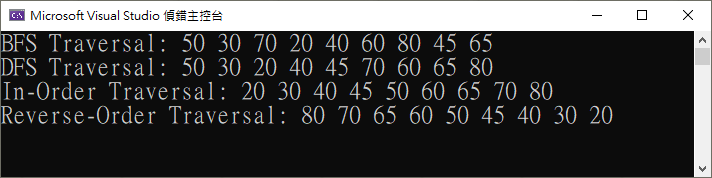
執行結果