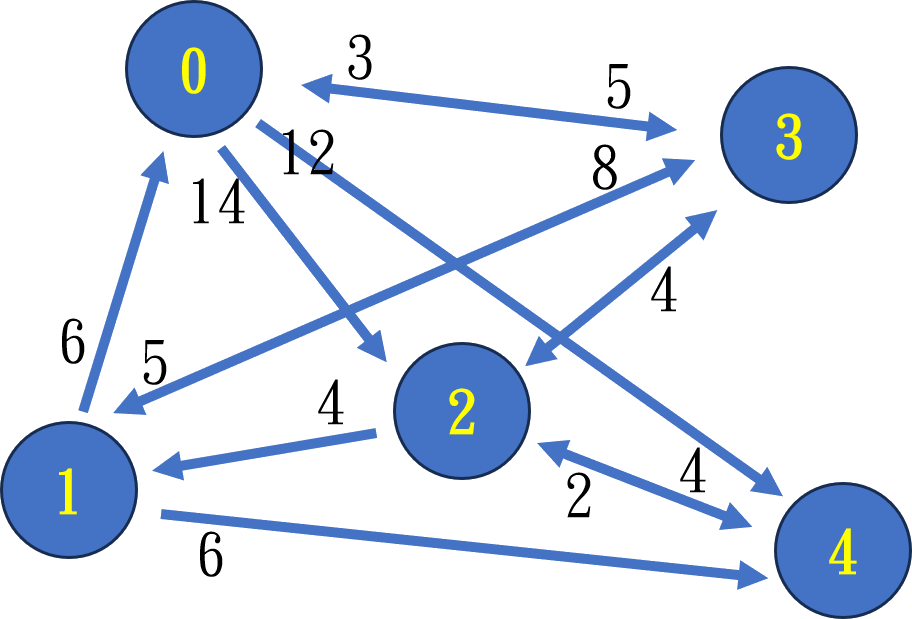
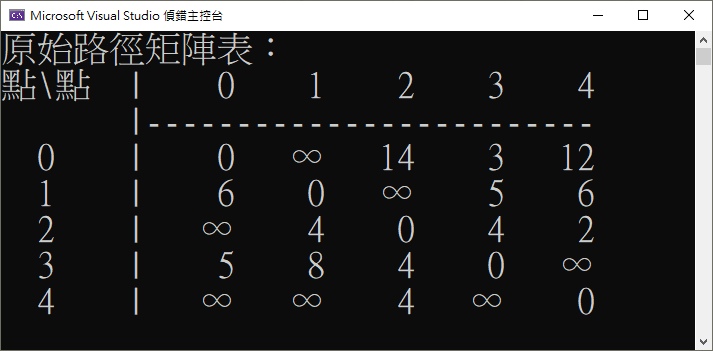
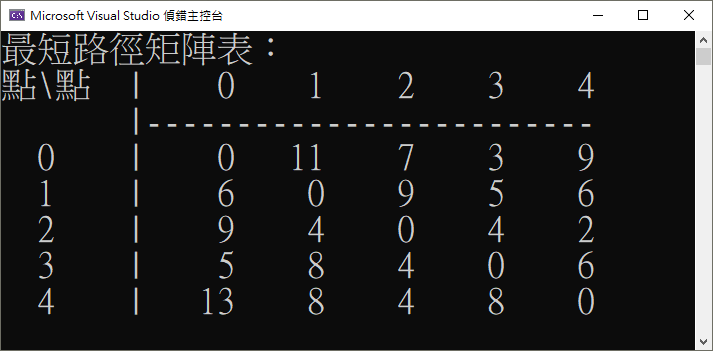
以下是 Floyd-Warshall 演算法的基本方法與特色:
- 初始設定: 初始化一個二維陣列 dist[][] 來表示從一個節點到另一個節點的最短距離。一開始,dist[i][j] 的值是從節點 i 到節點 j 的直接距離,如果有邊相連,否則為無窮大。同時,對角線上的元素(i 等於 j)設為 0。
- 三重迴圈: 使用三重迴圈遍歷所有節點,尋找可能的最短路徑。迴圈的目標是將每個節點作為中繼節點,檢查是否通過這個中繼節點可以縮短兩個節點之間的距離。
- 時間複雜度: Floyd-Warshall 演算法的時間複雜度為 O(V^3),其中 V 是節點數量。由於使用三重迴圈,演算法的效率可能在大型圖上受到一些限制。
- 所有節點對最短路徑: Floyd-Warshall 演算法能夠計算圖中所有節點對之間的最短路徑,而不僅僅是單一節點到其他節點的最短路徑。
- 動態規劃: 這是一種動態規劃的演算法,通過不斷優化子問題的解,最終得到整個問題的最優解。
- 遞推: Floyd-Warshall 演算法通過遞推的方式計算最短路徑,每一步都基於前一步的計算結果。
- 適用於包含負權邊的圖: 不同於 Dijkstra 演算法,Floyd-Warshall 演算法能夠處理包含負權邊的圖,但可能無法處理包含負環的情況。
using System;
class ShortestPathAlgorithm
{
const int NoPath = int.MaxValue; // 定義表示無路徑的值
/// <summary>
/// 輸出矩陣內容列表
/// </summary>
/// <param name="dist">最短路徑地圖陣列</param>
static void PrintSolution(int[,] dist)
{
int V = dist.GetLength(0);
Console.WriteLine("最短路徑矩陣表:\n點\\點 | 0 1 2 3 4\n |-------------------------");
for (int i = 0; i < V; ++i)
{
Console.Write($" {i} |");
for (int j = 0; j < V; ++j)
{
if (dist[i, j] == NoPath)
Console.Write(" ∞");
else
Console.Write($"{(dist[i, j] == 0 ? " 0" : dist[i, j].ToString().PadLeft(5))}");
}
Console.WriteLine();
}
}
/// <summary>
/// Floyd-Warshall 演算法,求出所有點至各點最短路徑
/// </summary>
/// <param name="graph">地圖陣列</param>
static void ApplyFloydWarshall(int[,] graph)
{
int V = graph.GetLength(0);
int[,] dist = new int[V, V];
Array.Copy(graph, dist, graph.Length);// 初始化最短路徑矩陣
// 遍歷所有節點,考慮每一個節點作為中繼節點的情況
for (int i = 0; i < V; ++i)
{
for (int j = 0; j < V; ++j)
{
for (int k = 0; k < V; ++k)
{
// 如果節點 k 可以縮短從 i 到 j 的距離,則更新最短距離
if (dist[i, k] != NoPath && dist[k, j] != NoPath && dist[i, k] + dist[k, j] < dist[i, j])
dist[i, j] = dist[i, k] + dist[k, j];
}
}
}
PrintSolution(dist);// 輸出最短路徑矩陣
}
static void Main()
{
int[,] path = {
{0, NoPath, 14, 3, 12},
{6, 0, NoPath, 5, 6},
{NoPath, 4, 0, 4, 2},
{5, 8, 4, 0, NoPath},
{NoPath, NoPath, 4, NoPath, 0}
};
ApplyFloydWarshall(path);
}
}