家豪教學網工科賽程式設計教學 102 年第三題

題目:在地圖中搜尋最低成本路徑

問題描述

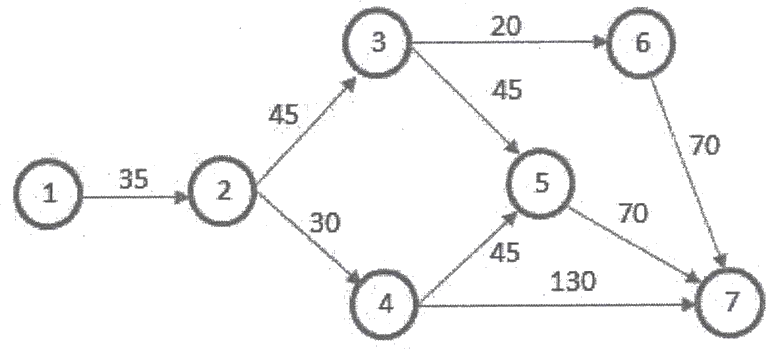
1. 如圖3一1所示為一交通示意圖，圓圈節點代表城市，並以數字表示其順序; 連接線表示城市間的行進方向，連接線的數字代表成本(成本 = 距離*時速 )。某君規劃假期將由出發地到目的地(如示意圖，由節點 ① 到節點 ⑦ ) ，假設城市間的各路段之距離及時速可事先查詢完成，則某君在出發前即可將各路段之距離及時速換算為成本 (如示意圖) ，據以搜尋最低成本的路徑，並處理得知其所經各城市節點的先後次序， 及其路徑的總和最低成本值。請設計一程式完成之。範例一 

   圖 3-1

2. 當城市間連接線的成本值改變，仍然可搜尋最低成本的路徑，並獲得其所經各城市節點的先後次序，及其路徑的總和最低成本值。

輸入格式：
1. 依序以「城市編號 城市編號 城市間連接線的成本數字」表示，例如：由節點 ① 到節點 ② 的表示為「1 2 35」。餘此類推，將所有城市及城市間連接線的數字設定完成，並存成輸入檔。
2. 輸入檔內容可隨時更改，格式如圖 3一2 所示



3. 可隨時更改輸入檔的成本值，再搜尋最低成本的路徑次序及其最低成本值。

輸出格式：印出最低成本值總和、其所經各城市節點的先後次序及其路徑值，如圖 3一3 所示：
範例二：
1. 節點 ⑥ 到節點 ⑦ 的值改為 70 ，如圖 3一4 所示：

輸入	正確輸出
範例一
1 2 35 2 3 45 2 4 30 3 5 45 3 6 20 4 5 45 4 7 130 5 7 70 6 7 100	最低成本值總和：180 路徑次序: 1 2 4 5 7 連線總值: 0 35 30 45 70

執行結果

輸入	正確輸出
範例二
1 2 35 2 3 45 2 4 30 3 5 45 3 6 20 4 5 45 4 7 130 5 7 70 6 7 70	最低成本值總和：170 路徑次序: 1 2 3 6 7 連線總值: 0 35 45 20 70

執行結果

輸入	正確輸出
範例三
1 2 13 1 6 2 1 7 18 1 4 7 2 3 1 2 7 3 3 2 2 3 4 5 3 7 6 4 5 2 4 7 10 4 3 4 5 4 3 5 7 13 5 6 12 6 7 14 7 1 1 6 5 1	最低成本值總和：15 路徑次序: 1 6 5 4 3 2 7 連線總值: 0 2 1 3 4 2 3

執行結果

using System; using System.Collections.Generic; using System.Linq; using System.IO; namespace _102_3 { class ShortestPathAlgorithm { public const int V = 7; //節點數量 public const int NoPath = -1;//無路徑 public const int OutFormat = 4;//輸出間格 public static int[][] path = Enumerable.Range(0, V).Select(_ => Enumerable.Repeat(NoPath, V).ToArray()).ToArray(); /// <summary> /// 讀取路線消耗成本檔案 /// </summary> /// <param name="filename">檔名</param> /// <param name="x">路徑地圖陣列</param> /// <returns></returns> public static bool ReadFile(string filename, ref int[][] x) { filename += (filename.ToUpper().Contains(".") ? "" : ".Txt"); //為文字檔加上 .Txt try { string[] lines = File.ReadAllLines("../../" + filename);//檔案位置在專案資料夾根部 for (int i = 0; i < lines.Length; i++) { string[] rowTemp = lines[i].Split(' ');//每列以空白隔開，最後字元不可空白 int a = int.Parse(rowTemp[0]); int b = int.Parse(rowTemp[1]); int c = int.Parse(rowTemp[2]); path[a-1][b-1] = c; } return (true); } catch (Exception ex) { Console.WriteLine($"An error occurred while reading the file: {ex.Message}"); return (false); } } /// <summary> /// 選擇未包含在最短路徑樹中，距離最短的節點 /// </summary> /// <param name="dist">起點至各點的最短距離</param> /// <param name="sptSet">已經拜訪過的點旗標</param> /// <returns>傳回索引值，起點至索引點為目前最短距離(扣除已拜訪過的點)</returns> public static int MinDistance(int[] dist, bool[] sptSet) { int min = int.MaxValue, minIndex = NoPath; for (int v = 0; v < dist.Length; v++) { if (sptSet[v] == false && dist[v] <= min) { min = dist[v]; minIndex = v; } } return minIndex; } /// <summary> /// 輸出起點到 dest 的最短路徑 /// </summary> /// <param name="dist">起點至各點的最短距離</param> /// <param name="parent">最短路徑連結</param> /// <param name="dest">目標點</param> public static void PrintSolution(int[] dist, int[] parent, int dest) { List<int> La = new List<int>(); Stack<int> St = new Stack<int>(); int a, b; Console.WriteLine($"最低成本值總和：{dist[dest]}"); Console.Write("路徑次序:"); La.Add(0); int i = dest; while (parent[i] != NoPath) St.Push(i = parent[i]); Console.Write(((a = St.Pop()) + 1).ToString().PadLeft(OutFormat)); while (St.Count > 0) { Console.Write($" {((b = St.Pop()) + 1).ToString().PadLeft(OutFormat)}"); La.Add(path[a][b]); a = b; } Console.WriteLine($" {(dest + 1).ToString().PadLeft(OutFormat)}"); Console.Write($"連線總值:"); foreach (int v in La) { Console.Write($"{v.ToString().PadLeft(OutFormat)} "); } Console.WriteLine(path[a][dest].ToString().PadLeft(OutFormat)); } /// <summary> /// Dijkstra 最短路徑 /// </summary> /// <param name="graph">地圖陣列</param> /// <param name="src">起點</param> /// <param name="dest">終點</param> public static void Dijkstra(int[][] graph, int src, int dest) { // 初始化起始點至各點最短距離為無窮大，最短路徑已拜訪標記為 false，父節點為 NoPath int[] dist = Enumerable.Repeat(int.MaxValue, graph[0].Length).ToArray();//距離 bool[] sptSet = Enumerable.Repeat(false, graph[0].Length).ToArray();//父節點 int[] parent = Enumerable.Repeat(NoPath, graph[0].Length).ToArray();//最短路徑標記 dist[src] = 0; // 起始節點到 src 自身的距離為 0 for (int count = 0; count < graph[0].Length - 1; count++) // 主循環，找到最短路徑 { int u = MinDistance(dist, sptSet); // 選擇未包含在最短路徑樹中，距離最短的節點 sptSet[u] = true; // 將選定的節點標記為已納入最短路徑樹 for (int v = 0; v < graph[0].Length; v++) // 更新相鄰節點的最短距離 { // 檢查節點是否未包含在最短路徑樹中，是否有邊相連，是否有更短的距離 if (!sptSet[v] && graph[u][v] != NoPath && dist[u] != int.MaxValue && dist[u] + graph[u][v] < dist[v]) { dist[v] = dist[u] + graph[u][v]; //更新最短距離及父節點 parent[v] = u; //更新到 v 節點的路徑是從 u 點而來 } } } PrintSolution(dist, parent, dest); //輸出最短距離及路徑 } static void Main() { if (!ReadFile("102-3Data1.txt", ref path)) return; if (0 != V-1) Dijkstra(path, 0, V-1); } } }