題目：多矩陣相乘運算次數

1. 兩個矩陣乘法運算必須滿足 A 矩陣的行數 (2) 等於 B 矩陣的列數(2)才可以相乘。例如A_3X2 X B_2X3
給定 n 個矩陣 M₁，M₂，M₃，M₄，…，M_n，執行矩陣相乘運算，其中，每一矩陣之行數(column) 與列數 (row) 均不大於 100 ,且3 ≤ n ≤ 10。請你(妳)設計一程式能輸入 n 個可相乘矩陣大小，找到這些矩陣相乘時(M₁×M₂×M₃×M₄×…×M_n)具有最佳結合次序，求得最少的乘法運算次數，及顯示這些矩陣相乘之結合次序，以節省計算成本。如下圖所示。參考範例:
假設共有 3 個矩陣 M₁，M₂，M₃ 要執行矩陣相乘運算，其中M₁為(10 × 100)矩陣、M₂為(100 × 5) 矩陣、M₃為(5 × 50) 矩陣，因為矩陣乘法具有結合性，所以，M₁(M₂M₃) = (M₁M₂)M₃，故我們可以用兩種方法進行運算，分別求算其乘法運算次數。
1. 以 M₁(M₂M₃)進行矩陣相乘時，其乘法運算次數計算如下：
M_{2(100 × 5)}M_{3(5 × 50)}= P_{(100 × 50)}，所需要之乘法運算次數: 100 x 5 x 50 = 25000
M₁ (M₂ M₃)= M_{1(10 × 100)}P_{(100 × 50)}= Q_{(10 × 50)}，所需要之乘法運算次數: 10 x 100 x 50 = 50000
乘法運算次數總計為: 25000 + 50000 = 75000
2. 以 (M₁M₂)M₃進行矩陣相乘時，其乘法運算次數計算如下：
M_{1(10 × 100)}M_{2(100 × 5)}= P_{(10 × 5)}，所需要之乘法運算次數: 10 x 100 x 5 = 5000
(M₁ M₂) M₃= P_{(10 × 5)}M_{3(5 × 50)}= Q_{(10 × 50)}，所需要之乘法運算次數: 10 x 5 x 50 = 2500
乘法運算次數總計為: 5000 + 2500 = 7500

故矩陣相乘次序應為(M₁ M₂) M₃，且最少乘法運算次數為 7500 次，以獲得最少之計算成本。運算次數結果顯示在畫面上,如下面的圖所示:





輸入格式	輸出格式
第一列為矩陣數量 第二列以後依序為每一個矩陣的列與行數量。	第一列輸出結合運算的字串。 第二列輸出運算次數。




範例一
輸入	正確輸出
3 1 100 100 5 5 50	<<M1 M2> M3> 7500




範例二
輸入	正確輸出
10 4 4 4 7 7 9 9 11 11 12 12 13 13 15 15 16 16 20 20 30	<M1 <M2 >M3 >M4 <M5 <M6 <M7 <M8 <M9 M10>>>>>>>>> 37350




範例三
輸入	正確輸出
6 30 9 9 100 100 8 9 99 99 10 10 60	<<M1 <M2 M3>> <<M4 M5> M6>> 36489


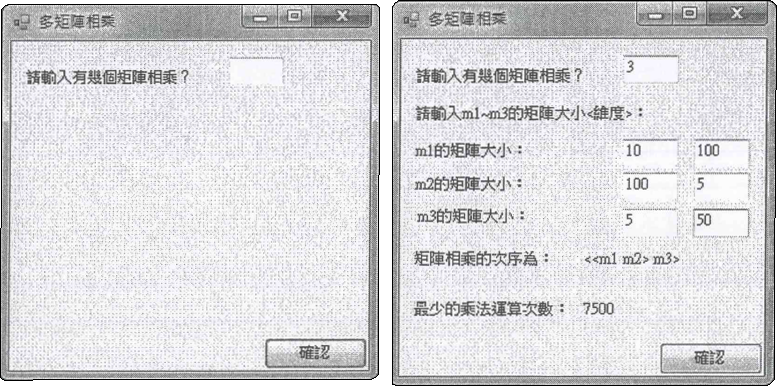
完成後影片


程式碼下載(GitHub)      程式碼下載(本地)


Microsoft Visual Studio Community 2022 (64 位元) - Current 版本 17.8.1