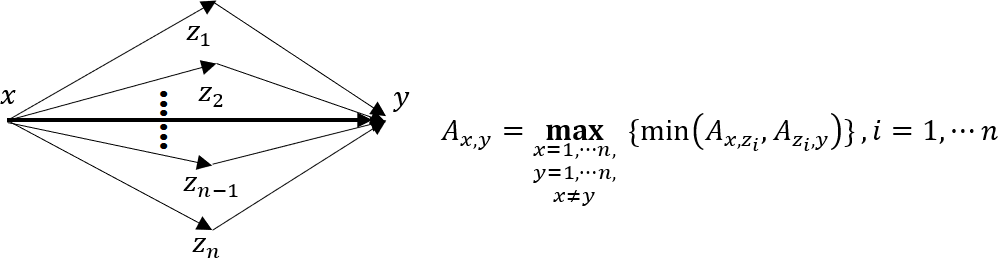說明：有一資訊系統在處理的過程中，其會產生對稱矩陣 An⨯n，如下所示。主對角線的值均為1，其餘的值介於0與1之間，值越大表示可信度越高，其中 Ax,y = Ay,x，x = 1,...,n，y = 1,...,n, x ≠ y，表示元素值 Ax,y 及 Ay,x 對稱於對角線。

1.00 0.63 0.53 0.57 0.47 0.50 0.47 0.68
0.63 1.00 0.53 0.30 0.40 0.43 0.47 0.60
0.53 0.53 1.00 0.40 0.50 0.57 0.47 0.51
0.57 0.30 0.40 1.00 0.53 0.47 0.40 0.52
0.47 0.40 0.50 0.53 1.00 0.50 0.43 0.52
0.50 0.43 0.57 0.47 0.50 1.00 0.43 0.40
0.60 0.47 0.47 0.50 0.43 0.43 1.00 0.43
0.68 0.60 0.51 0.52 0.52 0.40 0.43 1.00

以下為求出此資訊系統的矩陣分割值的步驟：
一、假設遞移律(Transitive closure)成立，使用遞移律運算此對稱矩陣以得到新的矩陣。遞移律的運算如下： 

1. 例如：求 A_2,5 的元素，先求 min( A_2,1, A_1,5 ), min( A_2,2, A_2,5 ), …, min(A_2,8, A_8,5 ), 之後，再求這 8 個數值的最大者，即為此 A_2,5 元素的使用遞移律運算結果。
2. 同樣方法對 A_1,2, A_1,3 , …, A_1,8, A_2,1, A_2,3, …, A_2,8, A_3,1, A_3,2, A_3,4, …, A_8,1, A_8,2, …, A_8,7 做運算。
3. 此矩陣的所有元素執行完遞移律運算後，若有任一元素被更新，則重複執行步驟1及步驟 2。

經數次使用遞移律運算得到新的矩陣如下：

1.00 0.63 0.53 0.57 0.53 0.53 0.47 0.68
0.63 1.00 0.53 0.57 0.53 0.53 0.47 0.63
0.53 0.53 1.00 0.53 0.53 0.57 0.47 0.53
0.57 0.57 0.53 1.00 0.53 0.53 0.47 0.57
0.53 0.53 0.53 0.53 1.00 0.53 0.47 0.53
0.53 0.53 0.57 0.53 0.53 1.00 0.47 0.53
0.47 0.47 0.47 0.47 0.47 0.47 1.00 0.47
0.68 0.63 0.53 0.57 0.53 0.53 0.47 1.00

二、在對角線之右上三角形的各列求出最大值，如下：
0.68 0.63 0.57 0.57 0.53 0.53 0.47
三、對上述步驟所得每列最大值做由小到大排序(各值只出現一次)：
0.47 0.53 0.57 0.63 0.68

執行結果
例 1：輸入 1.txt


例 2：輸入 2.txt


執行結果：

範例一


範例二


檔案格式說明：
檔案只要輸入上三角部分即可。
測資：範例一檔案下載，範例二檔案下載，程式碼下載