| 105 第四題 圓周率的逼近求解 吾人可利用圓內接正 n 邊形的方式,以逼近法求出圓周率 π 的 近似值,其為內接正 n 邊形的面積除以半徑的平方;本題設定圓的 半徑為 2。 【提示】 1.已知兩邊長 a、b 且夾角為 c 的三角形面積公式為 又已知半徑 r 的圓面積公式為 π r2。 2.請注意所使用三角函式角度是「度度量」還是「徑度量」。 輸入說明 輸入正整數 n,其中 3 ≤ n ≤ 500000。 輸出說明 請直接設定圓的半徑為 2,輸出圓的內接正 n 邊形的面積值,以及此時求 得圓周率 π 的近似值。 計算結果需列到小數點以下第 6 位,第 7 位(含)以下直接捨棄。 |
 |
範例
| 輸入 | 輸出 1:圓內接正 n 邊形面積 | 輸出 2:圓周率 π 的近似值 |
| 4 | 8.000000 | 2.000000 |
| 200 | 12.564303 | 3.141075 |
說明:
1.電腦程式語言所用的角度單位是弳,非度量。
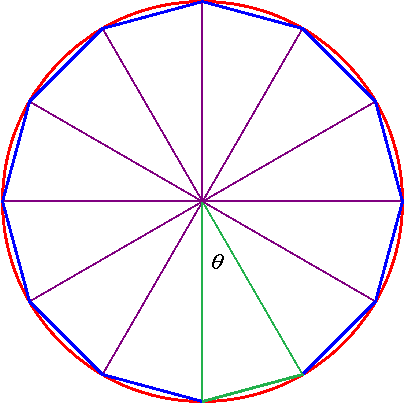
2.一個圓周角為 2π,若為 正 n 邊形,則有 n 個三角形,如下圖。
3.假設每一個三角形(綠色線)的內角為θ(靠圓心處),則 n 個三角形的內角,就有 nθ 。 nθ = 2π ,θ = 2π / n。
4.綠色線面積為 a∙b∙sinθ / 2 。
5.n 個三角形(等同綠色線三角形)的總面積為 n∙a∙b∙sinθ / 2 。
今 a、b 邊為圓半徑 r,故總面積為 n∙r2∙sinθ / 2 。
6.一個圓面積為 πr2, 若 n 個三角形總面積等同於圓面積,則
πr2 = n∙r2∙sinθ / 2 ,π = n∙sinθ / 2