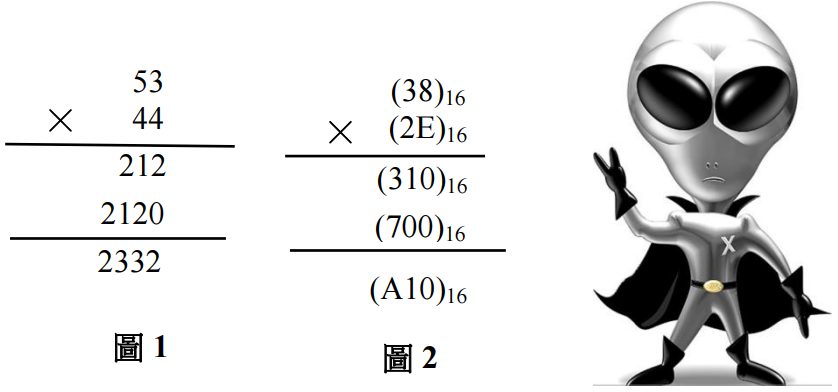
地球人是採用「十進位」系統,如圖 1 所示,我們利用「九九乘法表」進行乘法直式的 計算。據路邊社消息得知,冥王星人是採用「16進位」系統,所以如圖 2所示,需改用「FF 乘法表」進行乘法直式的計算。而 KIC 8462852 星球是在 2009 年首次被發現,位置離我 們約 1,500 光年遠,在銀河系天鵝座和天琴座之間,我們準備和其溝通,因此必須先準備 好 N 進位系統(N≦24), 開發能夠作 N 進位直式乘法的程式。註:當 N=24,則該數字系統 為 0123456789ABCDEFGHIJKLMN,均為大寫。
輸入說明
輸入 3個數值。第 1個數值代表要計算的進位系統 N,例如要進行 N=5進位,就輸入 5, 要進行 N=14進位就輸入 14;第 2、3個數值表示乘法直式運算的兩個數值,這兩個數值皆設 定為兩個位數;例如,若要進行 16進位計算,其數值範圍為 00~FF;各數字間以空格隔開。
輸出說明
輸出該 N進制直式乘法的 5個數值,各數字間以空格隔開;如圖 2的例子則輸出 "38 2E 310 700 A10";若輸入的運算數值不符合該進位系統,則輸出 "Error"。
範例
| 輸入 | 輸出 |
|---|---|
| 16 38 2E | 38 2E 310 700 A10 |
| 15 0A 1F | Error |
| 20 IJ AJ | IJ AJ I01 99A0 A7A1 |
分析
處理方式不管幾進制一律以 10 進制處理。
例如16進制 1C X 0B:
1C
x 2B
----------
第一列為 1C(16) x B(16) = 28(10) x 11(10) = 308(10) 放到 num[0]
第二列為 1C(16) x 20(16) = 28(10) x 32(10) = 896(10) 放到 num[1]
第三列為 前面兩列總和 308 + 896 = 1204 放到 num[2]
將 num 陣列內容分別轉回 n 進制輸出 (本例為 16 進制)
308(10)= 134(16)
896(10)= 380(16)
1204(10)= 4B4(16)
#define DigN 2 //定義長度
#define ERROR -1 //定義錯誤碼
#define ErrorMsg "Error\n" //定義錯誤訊息
using namespace std;
int N2Dec(string); //n 進制轉 10 進制
string Dec2N(int); //10 進制轉 n 進制
string Nmark = "0123456789ABCDEFGHIJKLMN"; //定義 24 進制以內各符號
int num[DigN + 1], n; //運算後結果
int main() {
string x = "", y = "", t = "";
int i, xn, k, u;
cin >> n;
cin >> x >> y;
//檢查長度是否為 2
if ((x.length() != DigN) || (y.length() != DigN)) {
printf(ErrorMsg);
system("pause");
return(0);
}
xn = N2Dec(x); //將 n 進制轉成 10 進制
//檢查超出 n
if (xn == ERROR) {
printf(ErrorMsg);
system("pause");
return(0);
}
//開始乘法運算
k = 1;
for (i = DigN - 1;i >= 0;i--) {
t = y.substr(i, 1);
u = (int)Nmark.find(t, 0); //檢查 y 非法字元
if (u >= n) {
printf(ErrorMsg);
system("pause");
return(0);
}
num[DigN - i - 1] = u * xn * k;
k *= n;
}
num[2] = 0;
for (i = 0;i < DigN;i++) //最後一列總和處理
num[DigN] += num[i];
cout << x << " " << y << " ";
for (i = 0;i <= DigN;i++)
cout << Dec2N(num[i]) << " ";
cout << "\n";
system("pause");
return 0;
}
//n 進制轉 10 進制
int N2Dec(string x) {
int i, j = 0, k = n, u;
string t;
for (i = 0;i < DigN;i++) {
t = x.substr(i, 1);
u = (int)Nmark.find(t, 0); //檢查非法字元
if (u >= n) return(ERROR);
j += u * k;
k /= n;
}
return(j);
}
//10 進制轉 n 進制
string Dec2N(int x) {
int u;
string t = "";
while (x > 0) {
u = x % n;
t = Nmark.substr(u, 1) + t;
x /= n;
}
return(t);
}