網路通訊時代,資料傳輸不免會有些雜訊干擾,為了讓通訊接收器可以偵測
與驗證資料 正確性,通訊傳送器常會在資料流 D中插入驗證碼的機制,得到一組
新的 codeword(碼字)。 例如,假設要傳送一組 M=8 位元資料 D = "11000010",
則加入驗證碼後的 codeword,可 由下列計算步驟求出:
A) 設定插入的驗證碼為 K個位元,其中資料長度M≦2n且 K = n + 1。編碼後的
codeword 長度則為 (M+K) 個位元。例如,若傳送的資料 D 為 M=8 位元,則驗
證碼長度為 K=(3+1)=4位元,codeword 總長度為 M+K = 8+4 = 12個位元。
B) 從左往右、由高位元至低位元,填入資料 D 的每個數位,但 2的次方的位置不填。
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 資料 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
C) 對「資料列」中 1的格子,在下方「二進位列」中,
寫入其「位置」的二進位值。
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 資料 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | ||||
| 二進位 | 0011 | 0101 | 1011 |
D) 對所有二進位數位,求「XOR(互斥或)」產生驗證
碼。0011⊕0101⊕1011 = 1101
E) 把產生之驗證碼「1101」,由低位至高位,依次填
入2的次方的位置(低位元在左)。
| 位置 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 資料 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | ||||
| 二進位 | 0011 | 0101 | 1011 | |||||||||
| 驗證碼 | 1 | 0 | 1 | 1 |
F) 碼字 codeword為上表所有底線數字的排列結果:"101110010010"
輸入說明
第一個數值為資料位元長度 K,介於 4~10 之間的整數;之後,輸入 K 位元之資料 D; 兩者以空格隔開。
輸出說明
輸出編碼後之 codeword。
範例
| 輸入 | 輸出 |
| 8 11000010 | 101110010010 |
| 8 10101101 | 011001011101 |
分析
A) 求 codeword 總長度為 M+K
求滿足 M≦2n 之 n 的方法有兩種.
1)使用對數函數.
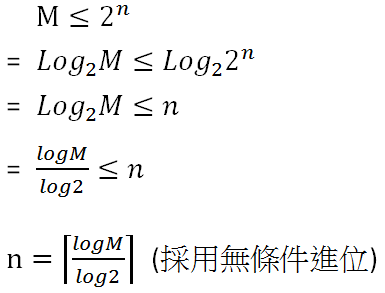
n = Math.Ceiling(Math.Log(m) / Math.Log(2))
注意:數學中的 Log 是以 10 為底,程式語言是以 e 為底。
2)使用迴圈計算.
n = 1
Do While n < m
n *= 2
Loop
B) 將資料填入 codeword 方法,可以將資料位置,存入陣列,方便使用。
Public tb() = {3, 5, 6, 7, 9, 10, 11, 12, 13, 14} "位置安排 (以 1 為起始)
For i = 0 To s.Length() - 1
Mid(ss, tb(i), 1) = s.Substring(i, 1)
Next
C,D) 題意步驟 C 其實可以省略,主要是取得驗證碼,因此只要針對是 1 的位元
處理 xor 就可以了。
Public tb() = {3, 5, 6, 7, 9, 10, 11, 12, 13, 14} "位置安排 (以 1 為起始)
x = 0 "步驟 C + D
For i = 0 To s.Length() - 1
If (s.Substring(i, 1) = "1") Then
x = x Xor tb(i)
End If
Next
E) 將驗證碼依次填入 codeword。( x 內容為驗證碼)
Public tb2() = {0, 1, 3, 7} "驗證碼位置 (以 0 為起始)
k = 1
For i = 0 To tb2.Length() - 1
Mid(ss, tb2(i) + 1, 1) = If((x And k) > 0, 1, 0)
k *= 2
Next
F) 輸出結果,ss 字串為結果,依序輸出至 Label.Text 即可。
Label1.Text = ""
For i = 0 To ss.Length() - 1
Label1.Text &= ss.Substring(i, 1)
Next