對於兩數值乘法運算,Anatolii Alexeevitch Karatsuba在 1960年發明
「透過拆分」 計算兩個 n 位數相乘的方法。下圖為計算 5678 × 1234的過程:
| a | b | |||||
| x= |
|
|||||
| y= | ||||||
| c | d | |||||
① 計算 a × c = 56 × 12 = 672
② 計算 b × d =78 × 34 = 2652
③ 計算 (a+b) × (c+d) = (56+78) × (12+34) = 6164
④ 計算 ③ - ② - ① = 6164 - 2652 - 672 = 2840
⑤ 計算 ① × 102×2 + ④ × 102 + ② = 7006652
首先將兩個數值拆分成 a、b、c、d 四個部分,分別計算 a×c 和 b×d 與
(a+b)×(c+d),最後再用第 3 計算式的結果,減去前面 2 個計算式,
然後在計算式 1 結果後面加 4 個 0(即 102×2),計算式 4 結果後面加 2 個 0(即 102),
再把三者相加,就是正確答案。
一般情況下,假設要相乘的兩個數是 x×y。我們可以把 x、y 寫成:
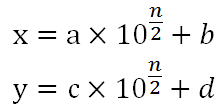
這裡 n 是數字的「位數」,如果 n 是偶數,則 a 和 b 都是 n/2 位數,
若數字是奇數位數,則令 n 設為該位數「減」1,例如 x=1234 (四位數)
則 n=4, a=12, b=34;若 x=12345 (五位數) 則 n = 5-1 = 4, a=123, b=45,
而 x=(a×102 + b)。之後 x×y 就變成:
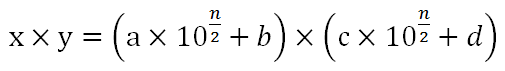
以上即為 Karatsuba 計算兩數乘積的方法;在程式實作上,需要注意的兩點是:
1. 這些乘法在程式裡可用「遞迴」實現,即當數字很大時先拆分,若拆分出來
的數字還是很大的話,就繼續拆分為 n/2,直到無法分拆為止,即當 x < 10
或 y < 10 時,停止拆分,直接回傳 x×y。
2. (a×d + b×c) 的計算為了避免兩次重複乘法,應該使用之前的「遞迴計算結果」。
3. 在遞迴函數中,依「① 式 --> ② 式 --> ③ 式」 順序作遞迴計算。
比如計算 12345 × 6789,拆分時 n = 5-1,a = 123、b = 45 以及 c = 67、d = 89,
也就是:12345 = 123 × 102 + 45 與 6789 = 67 × 102+89,那麼:
① 計算 a×c =123×67=8241
② 計算 b×d =45×89=4005
③ 計算(123+45)×(67+89)=26208
分析
| 這裡首先要更正上式運算式 | 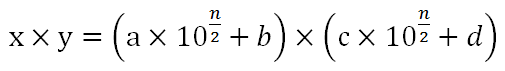 |
| 為 | 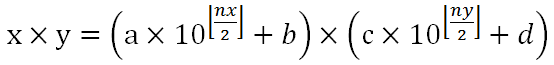 |
依此類推,ny \ 2,當 ny 為偶數,則 ny 直接取半,若為奇數,則 ny -1 再取半。
另外,⑤式必須更正。數理推導如下:
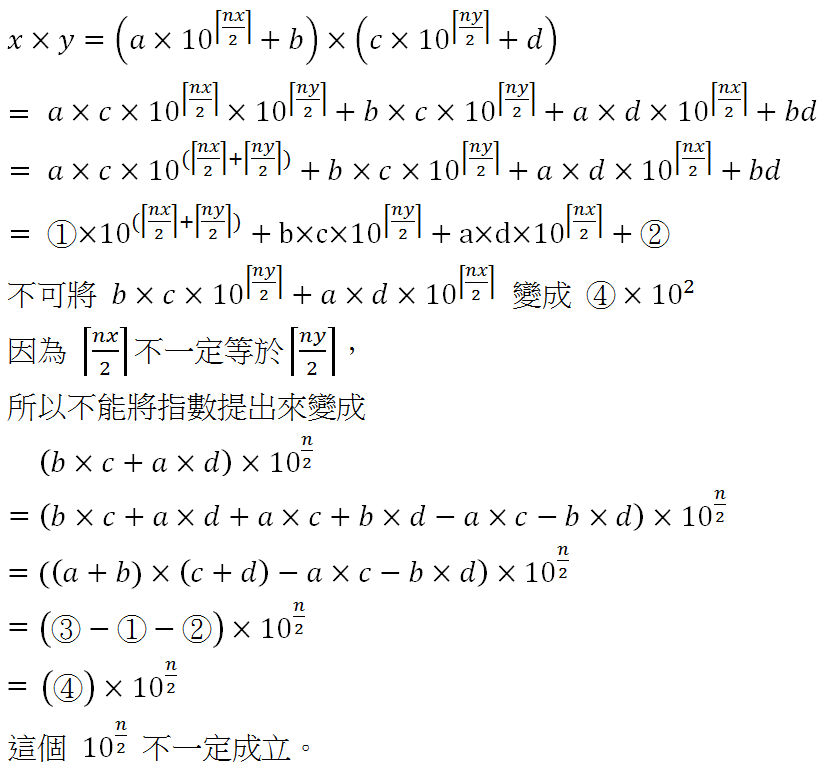
因此本程式之 ⑤ 並未照題意所提供式子完成。
| 本程式 ⑤ 為 | 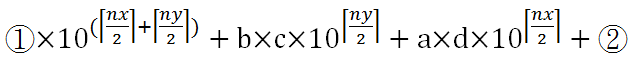 |
題中,
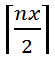 取法有兩種方式:
取法有兩種方式: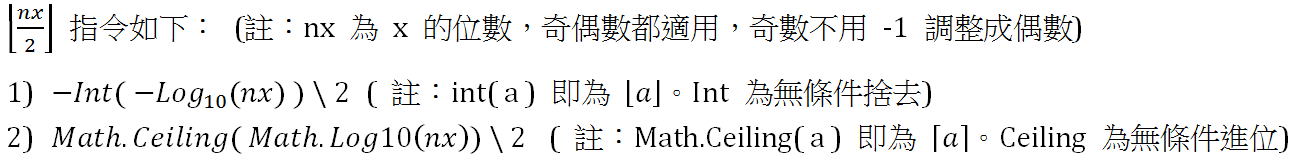
另外,本程式中取得 nx 以後,令 nx = nx \ 2,ny 同理。
運算子 \ 在 VB 環境中為整數除法 (無條件捨去小數除法)
寫遞迴式必須了解何事要重複做? 何時結束遞迴呼叫?
通常遞迴函數要先寫遞迴結束,再寫遞迴呼叫。
由題意之遞迴函數,大略步驟如下:
Function Karatsuba(ByVal x As ULong, ByVal y As ULong) As ULong
ListBox1.Items.Add("x=" & x & " , y=" & y) "輸出 x * y
If (x < 10 Or y < 10) Then "x 或 y 若為 1 位數,則結束遞迴傳回 x * y
Return (x * y)
Else
Dim a As ULong, b As ULong, c As ULong
Dim d As ULong, nx As ULong, ny As ULong
Dim ac As ULong, bd As ULong, abcd As ULong
Dim c5 As ULong
If (x = 10) Then "10 是特殊數字, 要特別處理
a = 1 : b = 0 : nx = 1
Else "將 x 拆成前後兩部分
nx = -Int(-Math.Log10(x)) \ 2
"求 X 位數 與 nx = Math.Ceiling(Math.Log10(x)) \ 2 等效
a = x \ (10 ^ nx) : b = x Mod (10 ^ nx)
End If
If (y = 10) Then "10 是特殊數字, 要特別處理
c = 1 : d = 0 : ny = 1
Else "將 y 拆成前後兩部分
ny = -Int(-Math.Log10(y)) \ 2 "求 y 位數 與 ny = Math.Ceiling(Math.Log10(y)) \ 2 等效
c = y \ (10 ^ ny) : d = y Mod (10 ^ ny)
End If
ac = Karatsuba(a, c) "① 計算 a × c
bd = Karatsuba(b, d) "② 計算 b × d
abcd = Karatsuba(a + b, c + d) "③ 計算 (a+b) × (c+d)
"⑤ 計算 ① × 10^(nx × ny) + a×d×10^nx + b×c×10^ny + ②
c5 = ac * 10 ^ (nx + ny) + ((a * d * (10 ^ nx)) + (b * c * (10 ^ ny))) + bd
Return (c5)
End If
End Function